Денешната Гугл чкртка (Google doodle) e посветена на една од најпознатите и, па и најстрашните формули во историјата на математиката – квадратната равенка. Формулата која веќе три илјади години ја дефинира рамнотежата помеѓу науката, историјата и секојдневниот живот, е наречена квадратна од мошне едноставни причини: затоа што непознатaтa x се појавува со експонент 2.
Напишана таа изгледа вака
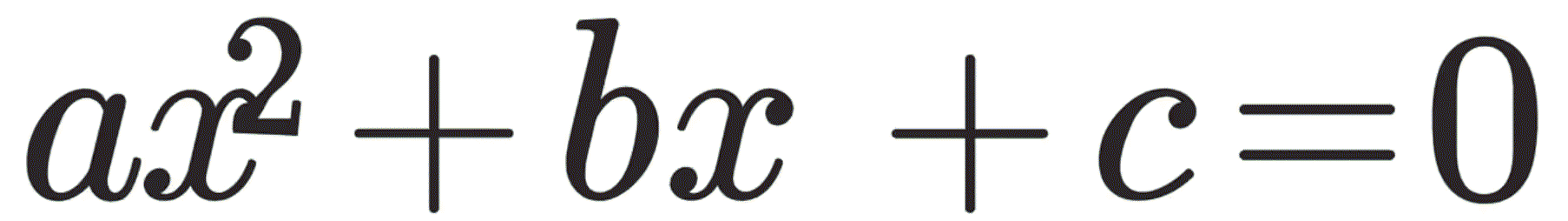
Зад овие симболи, кои многумина ги паметат од училиште, лежи еден од најгенијалните пронајдоци на човековата мисла. Тоа не е само формула: тоа е начин да се внесе ред во хаосот, да се пронајде скриен баланс, да се разбере кога едно нешто завршува, а друго започнува. Ова е “мајката на сите проблеми што се решаваат сами од себе“.
Долго пред компјутерите или пребарувачите да ја препознаат нивната елеганција, квадратните равенки веќе беа позната работа за астрономите, геометрите и за градителите. Пред три илјади години, Вавилонците решавале квадратни проблеми за пресметка на површина на земјиште или пак при мерење на дијагонални должини, иако сè уште немале современ симболички јазик.
Но, вистинската пресвртница доаѓа во 9-тиот век со Ал-Хаваризми, арапско-персискиот математичар од кого и потекнува зборот алгебра. Тој прв идентификувал општ начин за решавање на квадратните равенки. Во еден трактат, тој го опишува својот метод заснован врз дополнување и балансирање: односно, тој објаснува како да се „прекомпонира“ математичката рамнотежа, а терминот ал-џабр значи токму тоа – повторно составување на она што е скршено.
На некој начин, Гугл со деенешната “чкртка” го слави ембрионот на современата научна мисла: идејата дека проблемот, ако се донесе да биде „еднаков на нула“, може да најде решение.
Квадратната равенка се решава со формула што многу луѓе ја меморираат, честопати повеќе за... ритам отколку за разбирање:
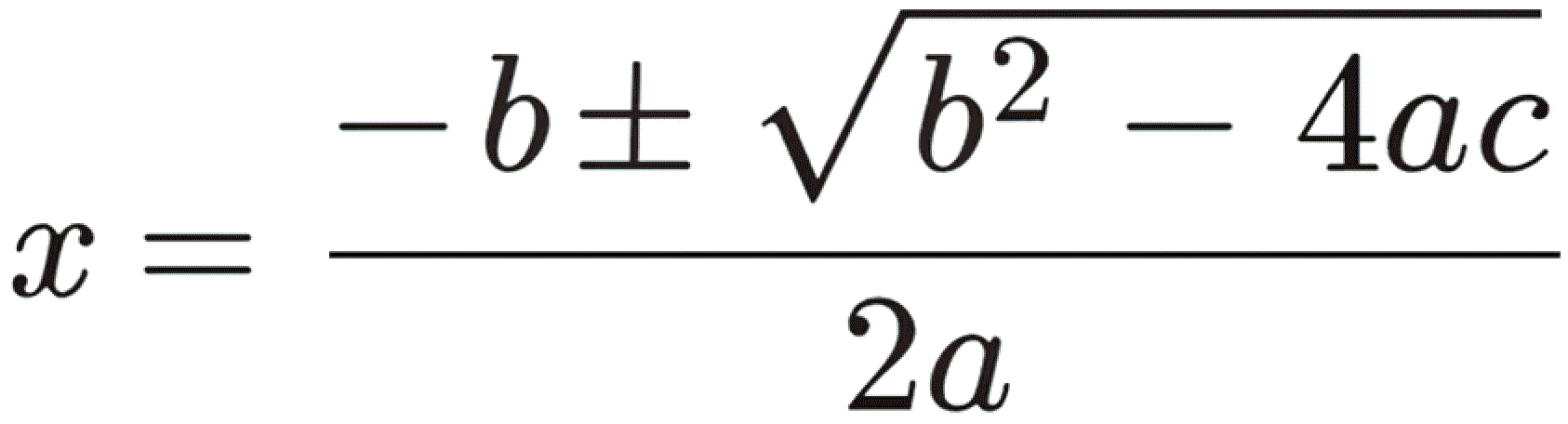
Терминот под квадратниот корен, делтата, одлучува сè: дали ќе има две решенија, само едно или дека нема вистинско решение. Се сеќавате на тоа, нели? Имаше нешто магично во моментот, во училиште, кога делтата се покажува како совршен квадрат: коренот „заокружен“, решенијата чисти, броеви што хармонично се вклопуваат. Тоа беше знак дека можеби решението на задачата одеше добро.
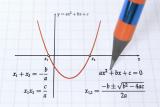
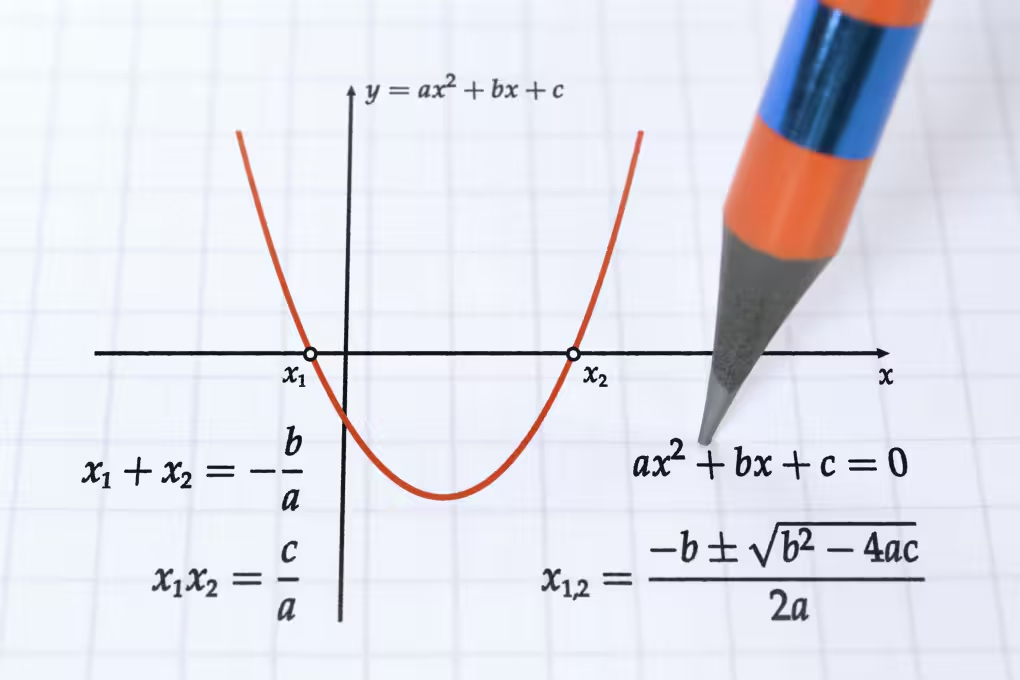
Но, овие решенија не се само “убави броеви”. Тие се точки на рамнотежа на реален феномен, моменти кога нешто „се враќа на нула“. Кога равенката е нацртана во координатен систем како парабола, точките каде што таа ја допира хоризонталната оска претставуваат решенија на равенката. Во тие точки, параболата „ја допира земјата“.
Само погледнете го ударот на кошаркарот, водата што се тече од фонтана или траекторијата на една ракета. Во сите овие случаи „природата“ следи параболичен закон. Објект лансиран во воздух се покорува на ова правило, а моментот кога ќе ја погоди земјата буквално претставува решение на квадратна равенка каде што непознатото е t, време.
Зад секој дневен гест – фрлање, испуштање, зрак светлина, стои мала „= 0“ што ја затвора приказната и го означува враќањето во рамнотежа.
Можеби универзалниот успех на квадратната равенка лежи во фактот дека таа е и елегантна метафора за светот. Сè што се раѓа, расте, достигнува врв, а потоа се спушта, ја следи на некој начин логиката на параболата. Тоа е кривата на куршумите и галаксиите, но и на одредени економски циклуси, моди, па дури и човечки страсти. Секој феномен има точка каде што силите достигнуваат рамнотежа, а потоа и спуштање кон нов почеток.
И така, кога денес го гледаме Google Doodle посветен на квадратната равенка, не славиме само дел од математичката историја, туку и формулата што нè потсетува на една едноставна, древна лекција: ако бараме решение, прво мора да поставиме сè да биде „еднакво на нула“. А потоа, којзнае, можеби ќе пронајдеме дури и две решенија ;)