За да добиете претстава за значењето на овој број, треба да се свртиме кон основите на компјутерската наука и Буловата логика. Буловата функција на влезот зема листа од искази „точно“ и „неточно“, а и на излезот дава еден „точен“ или еден „неточен“ исказ. Во две димензии, пример за Булова функција е онаа која враќа „точно“ кога барем еден од двата влеза е „точно“, и „неточно“ про неточен исказ. Буловите функции што тука ги интересираат истражувачите се монотони, односно во нив влезот се менува од неточно во точно, додека излезот не може да се промени од точно во неточно. Па овие Булови операции можеме да ги преформулираме со битови „0“ и „1“.

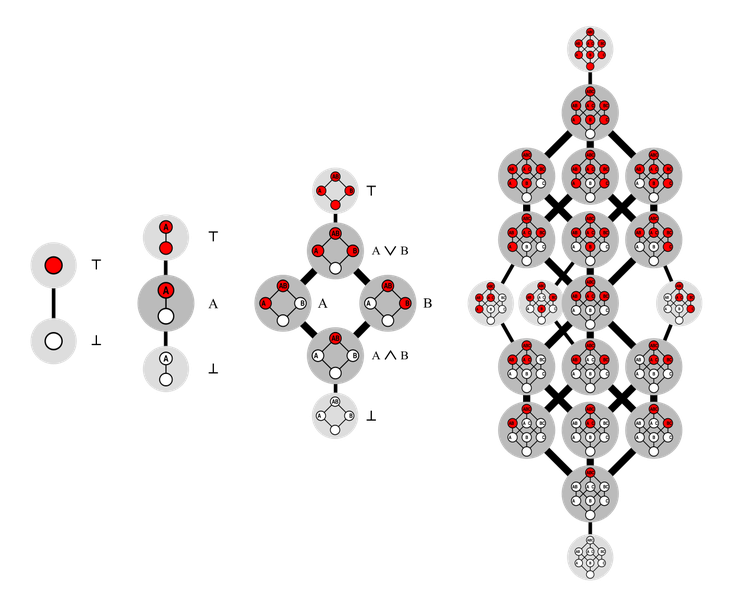
Илустрација на монотони Булови функции со 0, 1, 2 и 3 влезни членови. За вториот Дедекиндов број, постојат шест функции што одговараат на дефиницијата, вклучувајќи ја и онаа што враќа „точно“ ако барем еден од неговите два записи е точно (оваа функција е означена A ∨ B).

Воведен во 1897 година од страна на, погодивте, Рихард Дедекинд (Richard Dedekind), n-тиот Дедекиндов број е едноставно броење на монотони Булови функции со n влезни членови. „Потребни се само неколку искази за да се дефинираат монотоните Булови функции, но нивното броење е предизвик и за математиката и за компјутерската наука!“, вели Патрик Де Космакер (Patrick De Causmaecker). Со оглед на тоа што овие бројки растат двојно-експоненцијално, со брзина од 2^2^n, тие мошне бргу ги достигнуваат ограничувањата на пресметковниот капацитет на сегашните компјутери. Со растечката моќ на суперкомпјутерите и напредокот во математиката, приближно на секои триесет години се изнаоѓа нов член од бесконечната низа. Последниот Дедекиндов број беше пресметан во 1991 година од страна на Даг Видеман (Doug Wiedemann).

За да го пронајдат деветтиот Дедекиндов број, истражувачите, од една страна, го намалиле бројот на поими што треба да се пресметаат благодарение на оптимизацијата на формулата што ја користел Даг Видеман, а особено за да ги избегнат таканаречените „симетрични“ поими.

Од хардверска страна, „потрошивме година и пол дизајнирајќи наш сопствен компјутерски чип“, вели Ленар Ван Хиртум. Во повеќето случаи, истражувачите бираат помеѓу користење на обични (CPU) или графички процесори (GPU), за вршење на интензивни пресметки. „CPU, на пример, се повеќе оптимизирани за извршување на сложени операции, како што е множење, отколку за Булови операции“, објаснува компјутерскиот научник. Па така, тие се потпреле на еден друг вид на чип архитектура, којашто е помалку користена – FPGA (Field-programmable gate array), којашто е подобро прилагодена за прилично брзо изработување на ваков вид пресметки.

Но, како да бидете сигурни дека нема грешка во број испишан со 42 цифри? „Не можеме да го исклучиме тоа“, признава Патрик Де Космакер.

Случајно и за среќа, по неколку дена од нивната објава, на arXiv серверот се појави уште една публикација за деветтиот Дедекиндов број, во која при пресметките бил користен поинаков пристап и процесорска архитектура. Кристијан Џекел (Christian Jäkel) од Техничкиот универзитет во Дрезден го пресметал истиот број.

Шансите да се добие истиот број по грешка се исклучително ниски, па сосема извесно е дека обете пресметки се точно изведени. Па, во согласност на традицијата очекуваме дека за околу триесет години ќе имаме откровение на десеттиот Дедекиндов број