Постојат многу појави со исход „сé или ништо“, на пример положил/паднал на испит, се разболел/не се разболел, умрел/преживеал, колата издржала/се расипала итн. Иако исходот е бинарен („сé или ништо“), веројатноста за негово настанување може да зависи од некоја континуирана променлива. Ќе разгледаме три примери.
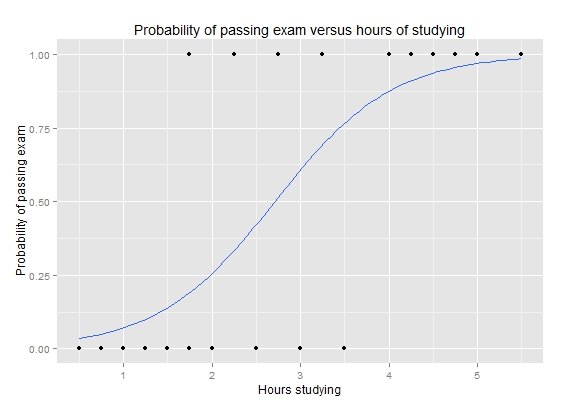
Прв пример: шансите за положување на испит во зависност од поминатите саати во учење (на подолниот дијаграм). Како што гледаме, сите коишто учеле помалку од 1,5 час паднале на испитот (на дијаграмот точките долу се паднатите). Како што се зголемува времето на учење, постепено има сé повеќе положени (точките горе), а се помалку паднати (точките долу). При 1,5 – 4 часа учење, има и положени и паднати. При повеќе од 4 часа учење речиси нема паднати на испитот. Иако исходот е бинарен (положен/паднат), веројатноста за положување се зголемува со времето на учење според кривата на логистичката (логит) регресија со сигмоидна форма (во форма на латиничната буква S). Уште се нарекува и Болцманова сигмоидна крива. Функцијата има два параметри и може да се нагоди за дадено множество податоци (стрмината на искачување на кривата и бројот часови на учење, каде кривата ќе го пресече нивото на веројатност од 0,5 на вертикалната оска).
Втор пример: шансите лицето да има дијабетес (шеќерна болест) во зависност од нивото на глукоза во крвта (на хоризонталната оска). Не постои една остра граница каде започнува дијабетесот. Мал број лица можат да имаат дијабетес уште при концентрација на глукоза од 6 mmol/l (на гладно). Во подрачјето помеѓу 6 и 7 mmol/l веќе има сé повеќе заболени (околу 6,5 mmol/l е централната, односно преодната точка на кривата). Над 90% од тестираните со концентрација на глукоза над 7 mmol/l веќе имаат дијабетес, иако понекој сé уште нема. Колку одиме подесно, сé поголема е веројатноста пациентот да има дијабетес (на пример над 8 mmol/l практично сите имаат дијабетес).
Значи, преминот не е е резок, не е сé црно-бело, односно она што често го кажуваат докторите, „2 плус 2 не се секогаш 4“. Всушност, секогаш се 4, ако се размислува преку веројатности и логистичка регресија. Тоа е така бидејќи сите луѓе не се исти, но сепак се забележува јасна закономерност на појавата, во смисла на веројатност.
Трет пример: процент на заразени од корона вирус во зависност од титарот на антитела во крвта. Иако нема реска граница, како што се зголемува титарот на неутрализирачките антитела во крвта, така расте веројатноста дека лицето нема да се зарази. Австралиските научници многу убаво ја моделираа таа крива и точно се знаат нивоата на антитела за разни веројатности од заболување. Затоа се чудам кога читам разни доктори кај нас, кои велат дека не се знае нивото на антитела кое е доволно за заштита. Навистина, нема реска граница, туку мора да се размислува преку веројатности за заразување. На пример, австралиските научници утврдиле дека постои 50% шанса за заразување ако титарот на наутрализирачки антитела опадне под 20,3% од титарот кај конвалесцентите. Зависно од применетата метода за мерење во нашите лаборатории, точно може да се пресмета ова ниво.
Заклучок: иако нема реска, црно-бела граница, за одредено ниво на веројатност (на пример 50% или 75% од популацијата) може да се постави границата за потребно ниво на неутрализирачки антитела. Тоа ниво ќе кажува дека 50% од луѓето ќе можат да се разболат, а 50% нема да се разболат при даденото ниво. Колку повисок титар – толку помала веројатност од заразување. Математички сé може да се опише, само треба некој пред сé тоа да го разбере.