Деновиве сè повеќе ненадејните смртни случаи се доведуваат во некаква врска со примена вакцина. Сега ќе видиме една пресметка базирана на теоријата на веројатноста и ќе видиме дека при масовна вакцинација ќе има многу случаи на случајно умирање од најразлични причини три дена по вакцинацијата, без никаква причинско-последична врска со примената вакцина.
Да ја земеме за пример Македонија, со 2,08 милиони жители и да претпоставиме дека 50% од населението (1,04 милиони) ќе биде вакцинирано во текот на една година. Поаѓајќи од бројот на смртни случаи минатата година (20.447), веројатноста за случајно умирање на било кое лице во било кој тродневен интервал изнесува P(A) = 20.443/2.080.000 * 3/365 = 0,0000808.
Веројатноста дека некое лице ќе биде вакцинирано во било кој тродневен интервал изнесува P(B) = 1.040.000/2.080.000 * 3/365 = 0,00411.
Веројатноста едно лице да примило вакцина и да умрело во даден тродневен интервал изнесува P(A)*P(B) = 0,000000332.
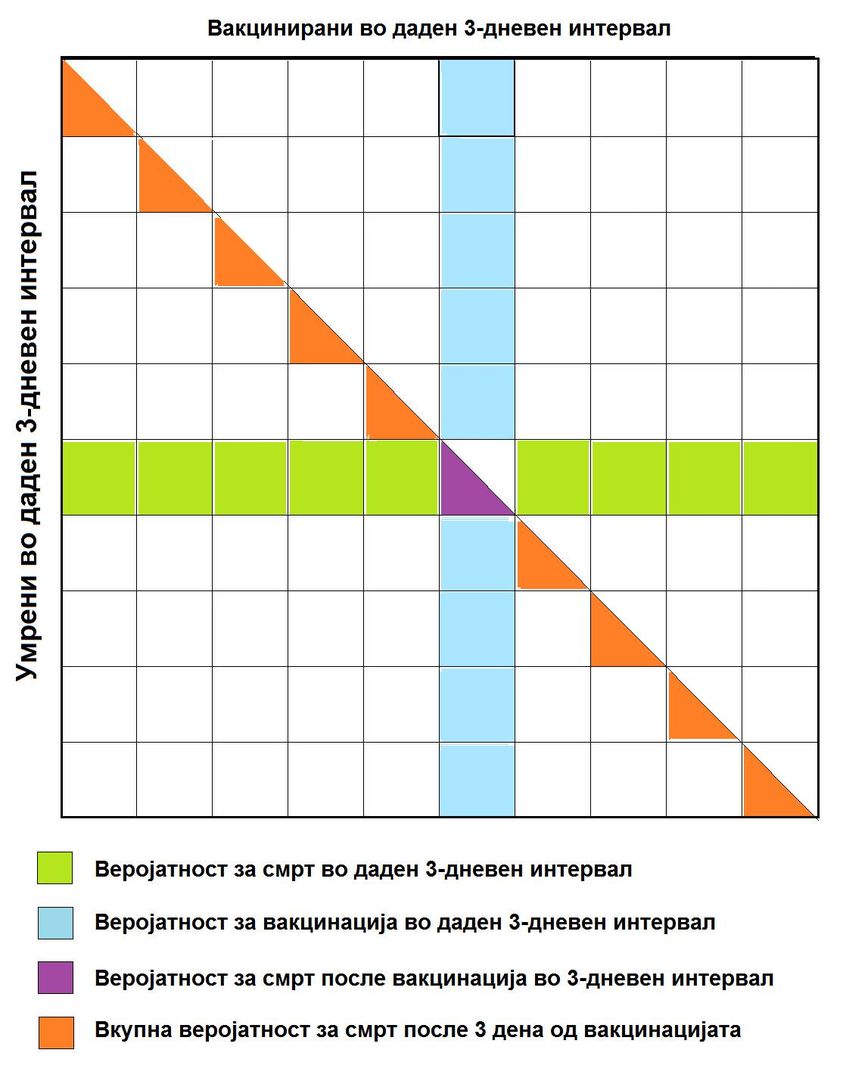Доколку овие два настани се случиле во еден тродневен интервал, веројатноста лицето прво да ја примило вакцината па умрело изнесува 0,5, а исто толку (0,5) изнесува веројатноста лицето прво да умрело и вакцината наменета за него да не ја примило. Така доаѓаме до веројатноста лицето да примило вакцина и случајно да умрело најдоцна три дена по примената вакцина во било кој тродневен времески прозорец: 0,5*P(A)*P(B) = 0,5*0,000000332 = 0,000000166.
Бидејќи во една календарска година од 365 дена има 365/3 = 121,7 тродневни интервали, веројатноста за смрт во рок од 3 дена по примена вакцина ПО ЧИСТА СЛУЧАЈНОСТ, односно поради временско совпаѓање на настаните (толку изнесува и пропорцијата на случаите во целата популација), изнесува p0 = 0,000000166*365/3 = 0,00002, односно 20 спрема милион, со стандардна девијација sp = 0,0000031 (добиено со статистички методи). Со други зборови, од 2,08 милиони вакцинирани по чиста случајност три дена по вакцинирањето во текот на годината би умреле околу 41,6 лица, плус или минус 12,6 лица (1,96 стандардни девијации на p0, помножено со 2,08 милиони жители), со доверливост од 95%, односно ризик од грешка од 5%.
Сè додека бројот на умрени до три дена по вакцинирањето во текот на цела година е помал од 54, таквото умирање се должи на случајно временско совпаѓање и нема основа да се доведува во врска со примената вакцина. Дури ако вкупниот број на умрени три дена по вакцинирањето во текот на целата година надмине 54 (односно четворица месечно), умирањето не било случајно и би можело да се прави анализа на причинско-последичната врска меѓу вакцинацијата и умирањето. На сликата е прикажана геометриска интерпретација на веројатноста, при што заради едноставност се земени само 10 тродневни интервали, но идејата е иста. Инаку, здравствените власти се обидуваат да селектираат за вакцинација само здрави лица, но секогаш им поминува по некој „под радарот“ кој ќе умре наскоро по примената вакцина, иако по чиста случајност.
Слична веројатносна анализа може да се направи за совпаѓањето на појавата на аутизам по примена MMR вакцина. Бидејќи двата настани се случуваат приближно во исто време, многумина кои не ги разбираат работите извлекуваат заклучок (како и сега со вакцините против ковид-19) дека вакцините предизвикуваат аутизам. Доколку би ги знаеле овие пресметки, би сфатиле дека се работи за чиста временска коинциденција, не би ширеле теории на заговор и на тој начин не би правеле штети по јавното здравје.
