До денес во Македонија од ковид-19 умреле 2.900 лица, односно околу 0,16% од популацијата од 1,8 милиони жители. Доколку тргнеме од средната стапка на леталитет (смртност) кај инфицираните во Европа од 0,77 % (таканаречен IFR - Infection Fatality Rate), тоа би одговарало на 20,8 % досега инфицирани, прележани и природно имунизирани лица. Дури и ако во едно лошо сценарио претпоставиме дека во Македонија стапката на леталитет е повисока заради лошото лекување (на пример IFR=1,0 %), стапката на прележаност е уште помала, одвај 16%. Серолошките испитувања во Шпанија, со која споделуваме многу слична кумулативна инциденца, покажале дека само 11% од населението поседува хуморален имунитет од антитела на SARS Cov-2 вирусот.

Да појдеме од оптимистичката и малку реална проценка дека досега прележалo 40 % од населението, што би одговарало на IFR= 0,4 %. Тогаш веројатноста на настанот А: „вирусот наишол на лице имуно од прележување“ ќе земеме да биде P(A) = 40 % = 0,4. Ако вкупната популација прикажана со големиот квадрат на првата слика, природно имунизираните се претставени со портокалова и зелена боја во долните 40 % од квадратот. Притоа, со зелена боја се означени прележаните кои подоцна би се вакцинирале, затоа што, како што рековме, не знаеле дека веќе прележале.

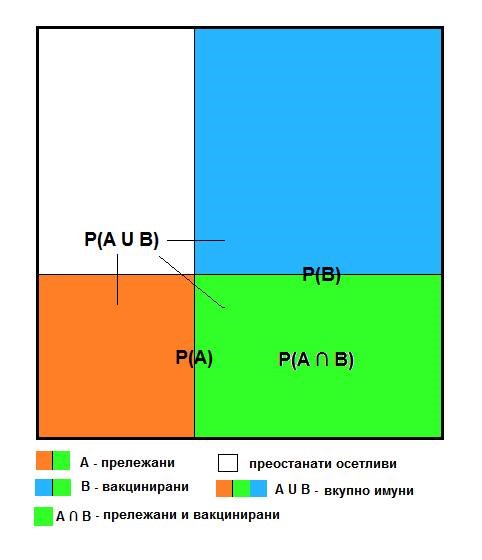
Сл. 1. Веројатност за имунитет од прележување и вакцинирање

Веројатноста на настанот В: „вирусот наишол на лице имунизирано со вакцина“ е непозната и неа сакаме да ја определиме, т. е. P(B) = x = ? . Овој удел ќе биде прикажан со сина и со зелена боја во десниот дел од големиот квадрат.

Вкупната веројатност на унијата на овие два настана A ∪ B: „вирусот наишол на прележано или вакцинирано лице“ треба да биде P(A ∪ B) = 75 % = 0,75. Имунизираните по двете основи ќе ги прикажеме со портокалова, зелена и сина боја и површината на обоениот дел од квадратот треба да изнесува 75% (согласно геометриската интерпретација на веројатноста).

Математичката веројатност на унијата (вкупниот имунитет од прележување или вакцинирање) ќе биде:

P(A ∪ B) = P(A) + P(B) - P(A ∩ B),

каде што P(A ∩ B) е веројатноста на пресекот на двата настана, т. е. лицето истовремено да прележало и да било вакцинирано. Нивниот удел го одземаме за да не го броиме двапати.

Бидејќи прележувањето и вакцинирањето се два независни настана (дел од асимптоматски прележаните ќе бидат вакцинирани, бидејќи не знаеле дека прележале), веројатноста на пресекот на двата настана е обичен производ на веројатностите, односно:

P(A ∩ B) = P(A) · P(B) = 0,4·x

Оттука првата равенка станува:

0,75 = 0,4 + x - 0,4·x,

со чие решавање добиваме:

x = P(B) = 0,58 = 58 %.

Понатаму, земајќи ја предвид ефикасноста на вакцините (ќе претпоставиме дека изнесува 95 %), доаѓаме до потребната минимална стапка на вакцинираност на населението: 58 % / 95 % = 61 %.

Значи, за да достигнеме стапка на имунизираност од 75 % потребно е да вакцинираме 61 %, а не само 35 %, што би се добило како проста разлика 75 % - 40 %. Од досегашните 40 % прележани користа нема да биде голема, бидејќи многумина од нив, поточно 40 %·58 % = 23,2 % од популацијата (зелената површина на скицата) ќе бидат вакцинирани и покрај тоа што прележале. Да се потсетиме, најголем дел од инфицираните (повеќе од 80 %) прележале асимптоматски.

Последната формула за x = P(B) сега можеме да ја генерализираме. Така ја добиваме формулата за потребниот опфат со вакцинација која гласи:

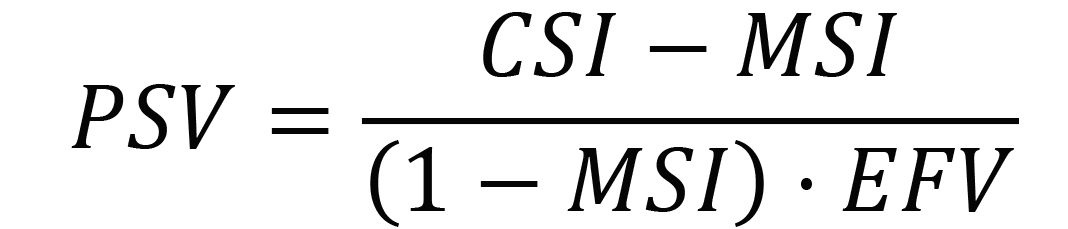
каде што:

PSV e потребната стапка, т. е. опфат со вакцинацијата,

CSI е целната стапка на колективен имунитет,

MSI е моментална стапка на имунитет од прележување,

EFV е ефикасноста на вакцината.

Вредностите на потребната стапка на вакцинираност (PSV), за разни целни стапки на имунитет и моментални стапки на имунитет од прележување ќе ги пресметаме и прикажеме табеларно и дијаграмски.

Сл 2. Потребна стапка на вакцинираност

Сега да разгледаме едно песимистичко, но многу реално сценарио, според кое само 21 % од населението стекнале имунитет со прележување, а целната стапка на колективен имунитет (поради повисоката преносливост на британскиот сој на вирусот) изнесува 90 %. Во овој случај ќе биде потребно да се вакцинираат дури (0,9-0,21)/(1-0,21)/0,95 = 0,92, односно 92 % од населението!

Јасно е без некакво големо докажување дека 92 % од популацијата нема да сака да се вакцинира на доброволна основа. Не заговараме принудна вакцинација, но да се потсетиме дека во 1972 година 90 % од населението на СФР Југославија било вакцинирано за само две недели. Едноставно државата ги повикала граѓаните да се јават на определените пунктови и граѓаните таму самите се јавувале, односно никој не бил присилно вакциниран. На тој начин, од избувнувањето на епидемијата во март 1972 до нејзиното сузбивање во мај поминале само два месеца!

Знаејќи какво е моменталното расположение кај населението, најверојатно ќе бидат вакцинирани најмногу 50 % од жителите, што би одговарало на вкупна стапка на имунизираност (заедно со прележаните 21 %) од 50 % + 21 % - 50 %·21 % = 60,5 %. Оваа стапка е точно на теоретскиот минимум за колективен имунитет од стариот сој на вирусот, но нема да биде доволна за имунитет на британскиот сој B.1.1.7. Во тој случај антиваксерите ќе продолжат спорадично да се заразуваат во текот на 2-3 години, сè додека не биде достигнато потребното ниво на колективен имунитет.

Инаку, ако сега вакцинираме само 20 % од популација, сметајќи со досегашна прележаност од 40 %, вкупната стапка на колективен имунитет би била само 40 % + 20 % - 40 %·20 % = 52 %, односно нема да постигнеме речиси ништо.

На крајот само да споменеме дека со одбивањето вакцинација, покрај тоа што самите антиваксери остануваат чувствителни на зараза (што за вакцинираните и прележаните, да речеме, не е важно), исто така му оставаат простор на вирусот да се шири и да создава нови, потенцијално поопасни мутации, од кои некоја може дури да биде отпорна на вакцини или да предизвикува огромна смртност. За ова сценарио здравствените власти треба сериозно да размислат и навреме да смислат начин за да вакцинираат доволен удел од популацијата.