Едно од неговите најголеми научни достигнувања е мерењето на големината на Земјината топка, со неочекувана прецизност.

Многумина ќе се изненадат кога ќе дознаат дека топчестиот облик на Земјата е откриен уште во античко време, пред повеќе од 2300 години, а откритието го направил античкиот филозоф Аристотел (384 – 322 пр.н.е.), кој навел неколку докази за тоа – бродовите „исчезнуваат“ во морето кога се оддалечуваат кон хоризонтот, Земјата секогаш фрла кружна сенка врз Месечината за време на затемнувањата на Месечината, а на различни географски ширини се гледаат различни соѕвездија на ноќното небо.

Иако сите антички филозофи од времето на Ератостен се сложувале дека Земјата е топка, никој не знаел колку е голема таа топка. Ератостен е првиот што ја измерил Земјината топка.

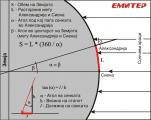
Интересен е начинот како тој го открил тоа – тој воочил дека на денот на летната долгоденица, на пладне, кога Сонцето е највисоко на небото, во градот Сиена (денешен Асуан) сончевите зраци го осветлуваат дното на еден бунар, додека во Александрија, којашто лежи северно од Асуан, тоа не се случува. Било очигледно дека на овие две локации, сончевите зраци на пладне паѓаат под различни агли, па за да ја утврди разликата во аглите, тој поставил вертикален стап во Александрија и според неговата должина и должината на сенката што тој ја прави, утврдил дека разликата во аглите изнесува α = 7°12' (види на слика 1).

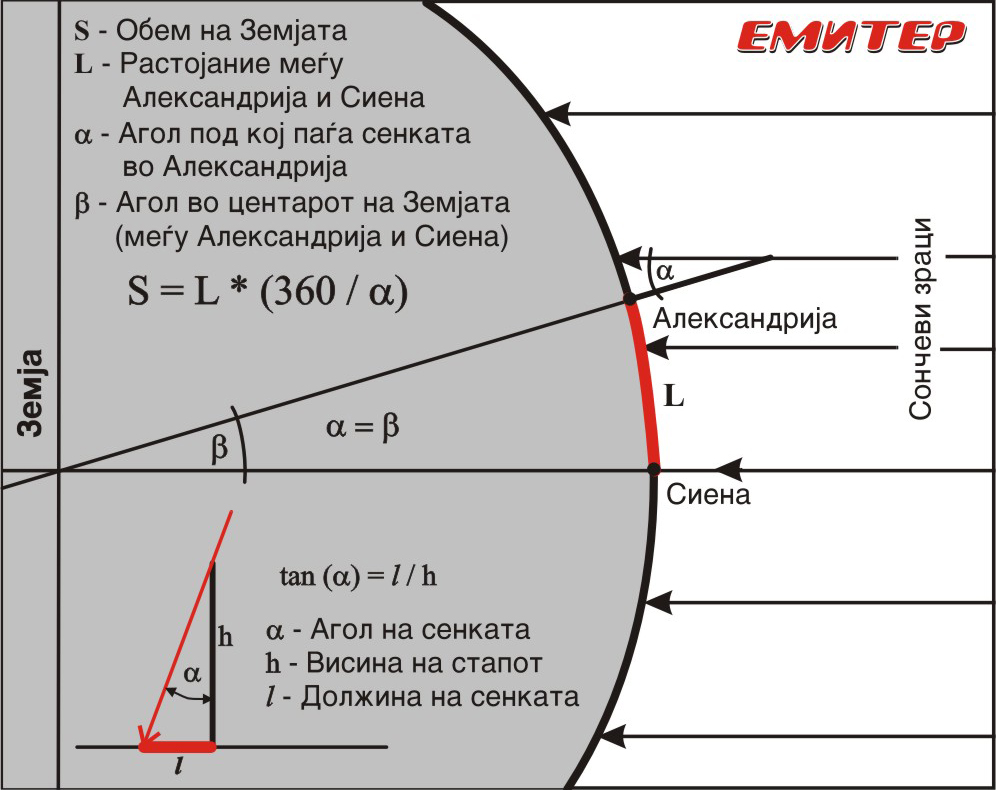
Слика 1: Ератостеновиот метод за пресметка на обемот на Земјата 

Веднаш сфатил дека таа разлика е последица од закривеноста на Земјата и дека растојанието помеѓу овие две локации не е праволиниско, туку е кружен лак, т.е. дел од меридијански круг опишан околу Земјината топка. Тоа сознание го инспирирало да го пресмета обемот на овој круг, но, за тоа му било нужно да го знае и растојанието L помеѓу Сиена и Александрија. За точно да го одреди растојанието помеѓу тие два града, платил еден т.н. бематист – човек чија професија била со воедначени чекори да мери растојанија помеѓу две локации. Така дознал дека растојанието помеѓу Сиена и Александрија изнесува L = 5000 „стадии“, односно L = 788,5 km. Конечно, со математичкото „просто тројно правило“, тој го пресметал обемот S на меридијанскиот Земјин круг. Еве ја неговата пресметка:

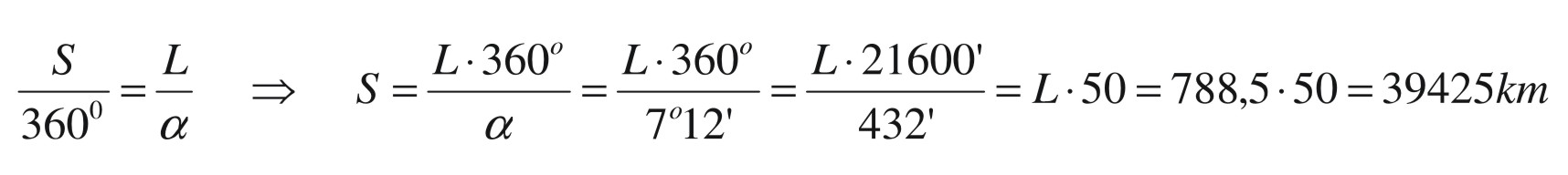
За споредба, според современите мерења, должината на меридијанскиот круг изнесува 40009,153 km, имено, таа се разликува од пресметката на Ератостен за само 1,5%. Фрапантна точност според условите коишто тој ги имал за точното одредување на нужните параметри: аголот на зракот и должината на кружниот лак. Притоа, Ератостен направил една мала непрецизност, бидејќи Сиена и Александрија не лежат точно на истиот меридијан, но тоа не влијае многу на резултатот.

Демонстрацијата на Ератостеновиот метод од Карл Саган

Овој интересен метод на Ератостен за откривање на заобленоста на Земјата, побудува интерес дури и во денешно време, како едноставен доказ за тоа дека Земјата е топчеста. Во ТВ-серијата „Космос“ од пред 40 години, којашто ја водеше познатиот физичар Карл Саган, тој нагледно го демонстрираше Ератостеновиот метод, така што употреби обичен картон на кој вертикално прицврсти две еднакво долги стапчиња. Осветлен од сончевата светлина, Карл Саган пред камерата покажува дека, кога картонската плоча е рамна, должините на сенките од стапчињата се еднакви, но кога го свитка картонот давајќи му кружен облик, сенките на стапчињата имаат различна должина, зависно од закривеноста на картонот, а во една дадена ситуација, едно од стапчињата воопшто нема сенка, аналогно како во случајот со Сиена. Оваа Саганова демонстрација читателите можат да ја видат во видеото дадено во прилог.

Ератостеновиот метод како ученички проект

Популарноста на Ератостеновиот метод побуди интерес и кај учениците од ООУ „Димитар Миладинов“ во Скопје. Имено, тие ја повториле Ератостеновата постапка, но помеѓу други две локации, едната во Скопје (во улога на Александрија), а другата во една точка на екваторскиот круг (во улога на Сиена).

Учениците од ООУ „Димитар Миладинов“ – Скопје го изведуваат Ератостеновиот метод

Експериментот го реализирале на датумот на рамнодневицата 21.03.2016 год., бидејќи на тој датум сончевите зраци паѓаат под вертикален агол 90° во точка на екваторскиот круг, која лежи на ист меридијан со Скопје, па во таа точка воопшто нема сенка (аналогно како во Сиена), додека во исто време во Скопје, според должина на сенката од стап висок 1 метар, тие утврдиле дека тука сончевите зраци паѓаат под агол од 42 степени. Растојанието помеѓу наведените две локации го дознале преку Google Earth, а го провериле според географска карта со размер 1 : 80000000, и така утврдиле дека тоа изнесува 4666,13 km. Знаејќи ги нужните параметри, разликата меѓу упадните агли и растојанието помеѓу двете локации, на ист начин, со примена на „просто тројно правило“, ја пресметале должината на меридијанскиот круг на Земјата, и добиле резултат 39995,399 km, многу близок до неговиот реален износ.

Браво за младите ентузијасти!