Истражувањето на квантната механика пред 100 години покажа дека сите честички можат да се категоризираат во 1 од 2 групи – бозони и фермиони. На која од групите ѝ припаѓаат честичките зависи од тоа како тие се однесуваат кога се во близина на други честички во дадена квантна состојба.

Но, една нова студија објавена во Nature предлага потенцијално постоење на трета група т.н. „парачестички“. Што ова значи?

Бозоните, како фотоните и Хигсовиот бозон, се покоруваат на Бозе-Ајнштајновата статистика. Ова значи дека во иста квантна состојба може да постојат неограничен број бозони.

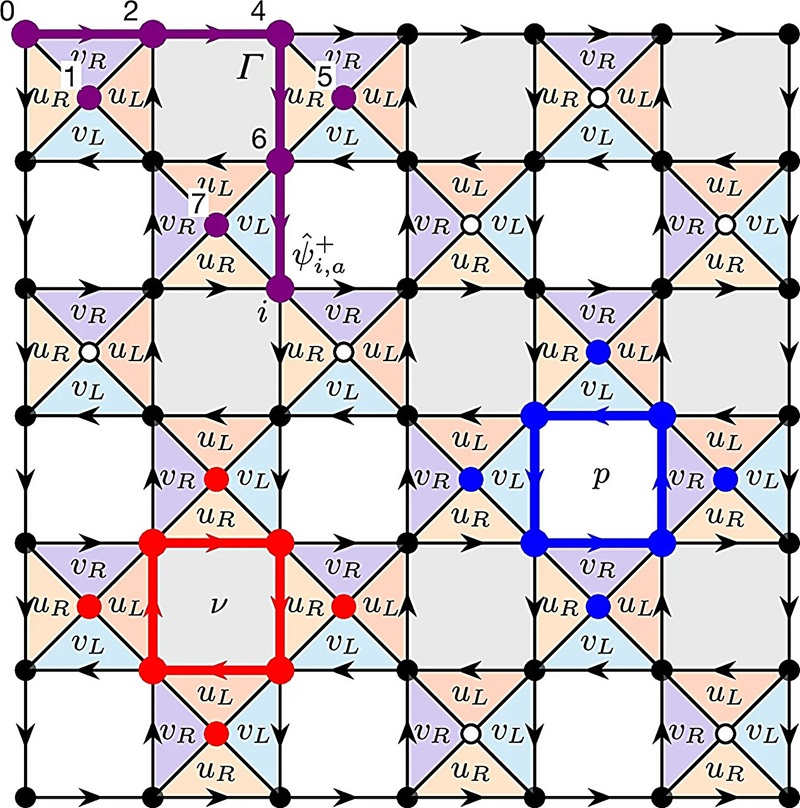
Tочно решлив 2D модел на спин на решетка 7 × 7 со отворени гранични услови. Преземено од Nature (2025), DOI: 10.1038/s41586-024-08262-7

Фермионите,  како електроните и кварковите, се управувани од статистиката на Ферми-Дирак. Ова значи дека само еден фермион може да се наоѓа во дадена квантна состојба. Токму ова однесување на фермионите, наречено принцип на Паули, ја одредува структурата на периодниот систем и е онаа причина „поради која што не се случува едноставно да поминете низ столот кога седнувате“, појаснува еден од авторите на трудот Каден Хазард (Kaden Hazzard) од Универзитетот Рајс во САД.

„Утврдивме дека е можно постоење на нови типови честички за кои никогаш порано не сме знаеле“, вели Хазард.

Имено, физичарите почнаа да шпекулираат за можно постоење на парачестички уште во 1930-тите и 1940-тите. Квантната теорија за овие честички беше формулирана во 1953 година.

Математичките студии покажаа дека речиси сите потенцијални парачестички всушност биле бозони или фермиони и се засновале на претпоставки кои по природа не се вистинити.

Хазард и Жијуан Ванг, поранешен студент на Универзитетот Рајс, ја истражуваа можноста за парачестички во квазичестичките – возбудена состојба кај материјали што имаат исти математички својства како честичките.

„Честичките не претставуват само основни работи“, објаснува Хазард. „Тие се подеднакво важни и за опишување на материјалите“.

Хазард и Ванг пронајдоа модели од системи на кондензирана материја во кои се појавуваат парачестички. Тие го направија тоа користејќи напредни математички пресметки, употребувајќи Лиева алгеба, Хопфова алгебра и служејќи се и со теоријата на репрезентација, како и сликовниот метод заснован на нешто познато како дијаграми на тензорски мрежи за подобро справување со равенките.

Иако истражувањето претставува важен момент во потрагата по парачестички, истражувачите ја нагласуваат потребата од конкретни докази. Па, откривањето на парачестички во лабораториски услови сосема извесно ќе потрае уште некое време.

„За реализација на парачестичките во експериментите, потребни ни се пореални теоретски предлози“, вели Ванг.

Космос