Дали обични 0,5-милиметарски трафо-лимови од силициумски челик за мрежни трансформатори можат да се користат (и со колкави загуби) за изработка на пригушница или трансформатор за 9000 Hz?
За жал, воопшто не можат, поради огромните загуби од магнетска хистереза и виорни струи, а за нивно мерење е осмислен следниот експеримент. На овие фреквенции сепак е задолжителна употребата на феритни јадра или дури намотки без јадра.
Загубите од хистерезисот и виорните струи, заеднички наречени загуби во железото, претставуваат реална загуба на моќноста, поради што во струјното коло се однесуваат како обичен отпор, слично како термогените (Џулови) загуби во бакарната жица од намотката. Еквивалентното коло на намотката, со импеданса Z1 , затоа го претставуваме со индуктивност L, сериски поврзана со отпорот RL на загубите во бакарот и железото (слика 1).
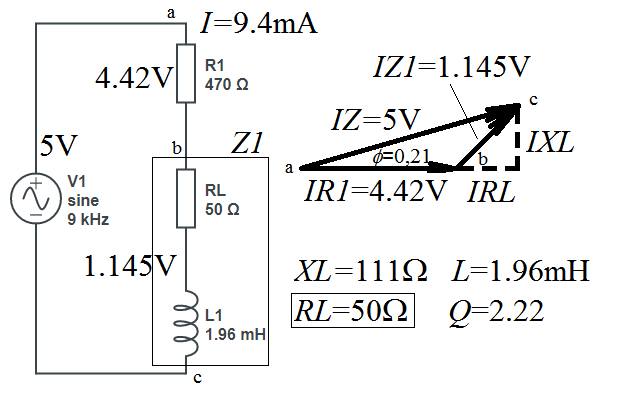
Слика 1: Експерименталното коло за мерење на отпорот на загубите, индуктивитетот и факторот на доброта на намотката.
Во експериментот струјното коло се состои од:
• пригушница со непозната индуктивност L и непознат отпор на загуби RL,
• сериски отпорник со познат отпор R1 = 470 Ω и
• синусен генератор за висока фреквенција f = 9000 Hz, со ефективен напон Ug = 5V.
Користиме векторски (фазорски) метод за анализа на колото. Доволни се три мерења на ефективните напони помеѓу точките a, b и c за да добиеме сé што ни е потребно. Овие 3 напони го формираат тапоаголниот триаголник Δabc, со познати страници, што ќе ни бидат доволни за понатамошна пресметка.

Слика 2: Намотката се состои од 30 намотки PVC-изолирана жица од 2,5 mm^2 на јадро EI-150 од 0,5 mm трафо-лимови од силициумски челик, наменети за мрежни трансформатори за 50 Hz. Пресекот на јадрото изнесува 25 cm^2. На 50 Hz намотката имала индуктивност од 26 mH, додека на 9000 Hz индуктивноста опаднала на само 1,96 mH. Индуктивноста опаднала бидејќи енергијата, наместо во магнетно поле, се претворала во топлина поради загуби од магнетска хистереза и виорни струи во железото. Q-факторот на намотката опаднал на само 2,22, додека кај воздушно намотана намотка би требало да изнесува барем 100
Отпорникот R1 ни служи само за да ја пресметаме ефективната вредност на јачината на струјата во колото, I = UR1/R1 = 4,42/470 = 0,0094 A = 9,4 mA.
Бидејќи намотката поседува отпор на загуби RL, векторите на напоните не формираат правоаголен, туку тапоаголен триаголник. Ова веднаш станува јасно, бидејќи за трите измерени напони 5 V, 4,42 V и 1,145 V не важи Питагоровата теорема.
Индуктивноста во колото прави падот на напонот на намотката I*Z1 фазно да доцни зад напонот на генераторот Ug =I*Z, што се гледа и од двоканалниот осцилограм на слика 3.
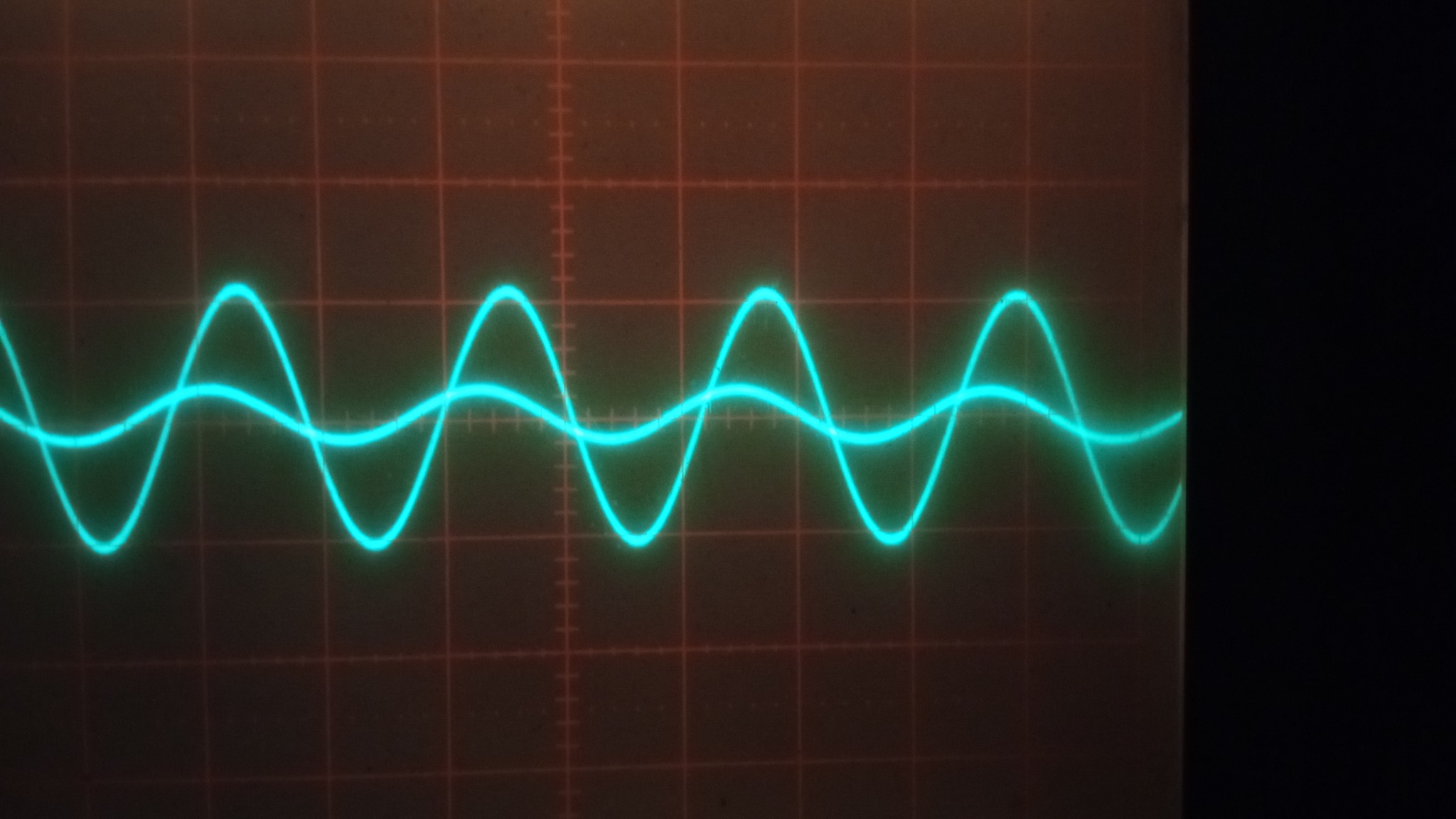
Слика 3: Осцилограми на двоканален осцилоскоп на напоните на генераторот и падот на напонот на намотката. Очигледно е фазното доцнење на помалиот напон (на намотката) во однос на напонот на генераторот. Напоните се претставени во еднаков размер
На слика 4 ја гледаме фигурата на Лисажу, каде хоризонталниот отклон на млазот на осцилоскопот е под дејство на напонот Ug , а вертикалниот е под дејство на падот на напонот на намотката I*Z1 (во еднаков размер). Овие две осцилации во два правци математички опишуваат елипса во параметарска форма. Доколку не би имало индуктивност, елипсата би дегенерирала во една коса отсечка.

Слика 4: Лисажуова фигура. Хоризонталниот отклон на осцилоскопот го преставува напонот на генераторот, а верткалниот отклон - падот на напонот на намотката. Поради фазното доцнење се појавува елипса, а хоризонталниот и вертикалниот распон се пропорционални на максималните напони на генераторот и намотката. Математички, овие два напони, коишто се менуваат по хармониски закон со фазно доцнење, претставуваат равенка на елипса во параметарска форма.
Да се вратиме на пресметките. Најпрво, со косинусна теорема од трите измерени напони (страниците на фазорскиот триаголник abc) го пресметуваме фазниот агол ϕ :
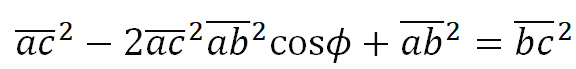 , од каде:
, од каде:
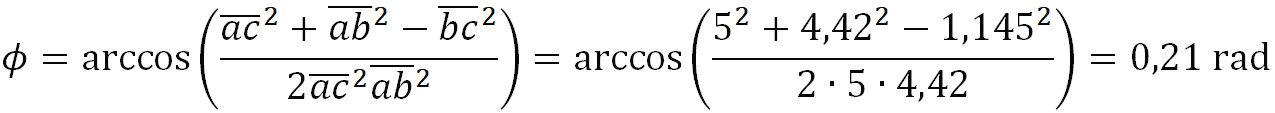
Потоа векторите ги проектираме во хоризонтален и вертикален правец (на реалната и имагинарната оска), имајќи предвид дека импедансата Z1 на завојницата се состои од отпор на загуби RL (реален дел) и индуктивна реактанса XL (имагинарен дел).
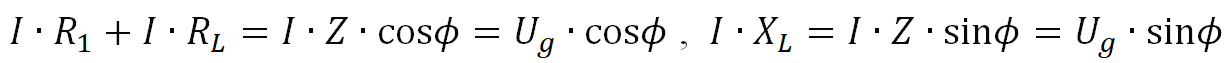
Од јачината на струјата I, напонот Ug и фазниот агол ϕ ги пресметуваме отпорот на загубите RL и индуктивната реактанса XL:
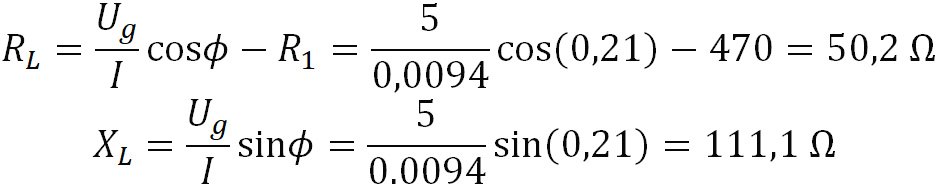
Со помош на кружната фреквенција ω = 2πf = 6,28 · 9000 = 56520s-1 го пресметуваме и индуктивитетот L = XL/ω = 111,1/56 520 = 0,00196 H = 1,96 mH.
Конечно доаѓаме до најважниот резултат, а тоа е Q-факторот (факторот на доброта) на завојницата, т.е. соодносот на индуктивната реактанса и отпорот на загубите:
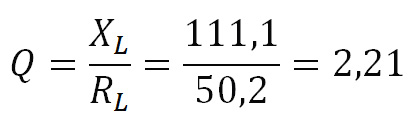
Толку нискиот фактор на доброта претставува катастрофално лош показател, бидејќи кај воздушно намотаните намотки на овие фреквенции се постигнуваат Q-фактори поголеми од 100.
Вториот заклучок го изведуваме од вредноста на индуктивноста. На 9000 Hz намотката има индуктивност од одвај 1,96 mH, иако на 50 Hz имала индуктивност од дури 26 mH. Ова покажува дека енергијата, наместо да се претвора во магнетско поле, се губи во магнетска хистереза и виорни струи.
Со следење на осцилоскоп не е забележано влегување на јадрото во магнетско заситивање (не се појавиле шилци на струјата). Заради малата должина на жицата Џуловите загуби се занемарливи и лесно се пресметуваат.
Заклучуваме дека обичните силициумски лимови со дебелина од 0,5 mm не можат да се користат за изработка на намотки за пригушници или трансформатори на фреквенција од 9000 Hz, барем не по цена на прифатливи загуби. Познато е дека загубите од хистереза растат пропорционално со фреквенцијата, но загубите од виорни струи растат со квадратот од фреквенцијата, но и со квадратот од дебелината на лимовите. Евентуално би дошло предвид користење на специјални лимови со дебелина од 0,1 mm (за аудио и сигнални трансформатори), иако феритните ZnMn јадра се вистинското решение на овие фреквенции.
На крај само да кажам зошто воопшто сум разгледувал примена на обични трафо-лимови на килохерцни фреквенции. Во склоп на проектот за предавателна антена за многу долги бранови (VLF – very low frequencies) потребна е намотка за прилагодување (loading coil) со индуктивност од 1,2 H, што ќе биде во состојба да издржи струја од најмалку 1 A.
Пресметките покажаа дека една огромна 10-слојна воздушна намотка, со висина 2 m и дијаметар 1 m, би требало да содржи вкупно 3 km бакарна жица, што е прескапо решение. Како една варијанта беше разгледано користењето на неколку намотки на јадра од трансформаторски лимови, но видовме дека ни тоа не доаѓа во предвид и тоа поради големите загуби.
На крајот останува решението со неколку намотки на затворени ZnMn феритни јадра за повисоки фреквенции, што сепак ќе биде поевтино, но и покомпактно од решението со воздушна намотка. Загубите во феритнот материјал би требало да бидат доволно мали, но сепак мерењата ќе го кажат главниот збор.
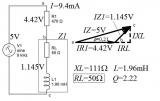
Слика 1: Експерименталното коло за мерење на отпорот на загубите, индуктивитетот и факторот на доброта на намотката.

Слика 2: Намотката се состои од 30 намотки PVC-изолирана жица од 2,5 mm^2 на јадро EI-150 од 0,5 mm трафо-лимови од силициумски челик, наменети за мрежни трансформатори за 50 Hz.
Пресекот на јадрото изнесува 25 cm^2. На 50 Hz намотката имала индуктивност од 26 mH, додека на 9000 Hz индуктивноста опаднала на само 1,96 mH.
Индуктивноста опаднала бидејќи енергијата, наместо во магнетно поле, се претворала во топлина поради загуби од магнетска хистереза и виорни струи во железото.
Q-факторот на намотката опаднал на само 2,22, додека кај воздушно намотана намотка би требало да изнесува барем 100
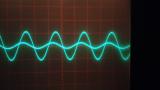
Слика 3: Осцилограми на двоканален осцилоскоп на напоните на генераторот и падот на напонот на намотката. Очигледно е фазното доцнење на помалиот напон (на намотката) во однос на напонот на генераторот. Напоните се претставени во еднаков размер

Слика 4: Лисажуова фигура. Хоризонталниот отклон на осцилоскопот го преставува напонот на генераторот, а верткалниот отклон - падот на напонот на намотката.
Поради фазното доцнење се појавува елипса, а хоризонталниот и вертикалниот распон се пропорционални на максималните напони на генераторот и намотката.
Математички, овие два напони, коишто се менуваат по хармониски закон со фазно доцнење, претставуваат равенка на елипса во параметарска форма.


