Имено, тој сфатил дека кружното движење е резултанта од две компоненти: првата е праволиниско движење со константна брзина на некое тело со занемариво мала маса, а втората е рамномерно забрзано движење на истото тело под дејство на силата на гравитација од некое друго, многу помасивно тело, која дејствува под прав агол на праволиниското движење на првото тело. Од законите на тие две компоненти се изведува законот за брзината којашто треба да ја има секое тело за да се движи кружно околу некое друго, многу помасивно тело. Ние нема да навлегуваме во изведување на таа постапка, туку директно ќе ја наведеме конечната формула за тој Њутнов закон;

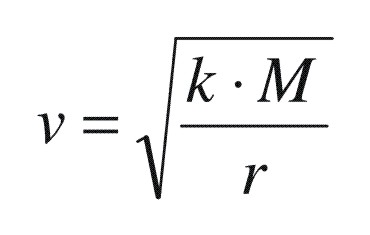
Каде што v е нужна брзина на телото за тоа да се движи кружно околу некое друго тело што има многукратно поголема маса M;

r – е растојание помеѓу центрите на тие две тела;

k – е гравитациска константа, изнесува 6,67428 · 10^-11  (Nm^-2kg²).

Левo: Опциите од дејството на Њутновиот топ; Десно: Сер Исак Њутн

Бидејќи нас нè интересира брзината за кружно движење околу Земјата, во формулата дадена погоре ќе ја внесеме масата на Земјата, која изнесува

M = 6 · 10²⁴ kg,

а како растојание помеѓу телата ќе го земеме најповолниот теоретски случај; екваторскиот радиус на Земјата, 6 378,1 km. Ако наведените параметри ги внесеме во формулата (1), и ја пресметаме, ќе го добиеме износот на брзината на телото, неопходна за кружно движење околу Земјата:

v = 7910 m/s (v = 7,91 km/s)

Оваа брзина е наречена “прва космичка брзина”, меѓутоа, јасно е дека во практиката вештачките сателити орбитираат околу Земјата во поширока орбита, со поголем радиус отколку што изнесува Земјиниот екваторски радиус. Имено, нивната орбита е над Земјината атмосферска обвивка.

Лево: Испукување на ѓулето со брзина далеку помала од 7910 метри во секунда; Десно: Испукување на ѓулето со брзина нешто помала од 7910 метри во секунда

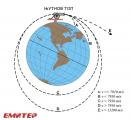
Поентата од сето досега кажано е во тоа што, врз основа на формулата (1) Њутн ја пресметал нужната брзина за кружно движење на некое тело околу Земјата, и со тоа ја предвидел можноста за лансирање вештачки сателит во орбитата околу Земјата. Но, во негово време технологијата не била во состојба да конструира ракетни мотори за досег до толку голема брзина, па Њутн се послужил со шеговита намисла; таа брзина да ја постигне со истрел од артилериски топ, способен да испукува ѓулиња со огромна брзина, поставен на височина над атмосферата на Земјата (види ја сликата во прилог). Оваа негова духовита шега популарно е позната под називот “Њутнов топ” (Newton's cannon). На цртежот се прикажани опциите од дејството на Њутновиот топ, а секоја од опциите можете да ја проследите и со соодветна анимација.

Лево: Испукување на ѓулето со брзина од 7910 метри во секунда; Десно: Испукување на ѓулето со брзина поголема од 11200 метри во секунда

При примена на помало барутно полнење, испуканите ѓулиња би имале помали брзини од наведената “прва космичка брзина” v = 7,91 km/s, па би паѓале на тлото на Земјата (случај A и B). Но, при соодветно поголемо барутно полнење, ѓулето би можело да биде испукано токму со “првата космичка брзина”, па во тој случај тоа би станало вештачки Земјин сателит кој кружно би орбитирал околу Земјата (случај C). Со уште поголемо барутно полнење, орбитата на ѓулето би преминала од кружна во елипсовидна (случај D). И, конечно, при екстремно големо барутно полнење на топот, ѓулето би можело да биде испукано со брзина поголема од 11,2 km/s, т.н. “втора космичка брзина” , па така тоа би излегло од досегот на Земјиното гравитациско дејство и би продолжило да се движи по хипербола, талкајќи низ космичкиот простор (случај E).

Сите овие опции се графички покажани на сликите во прилог, разгледајте внимателно!