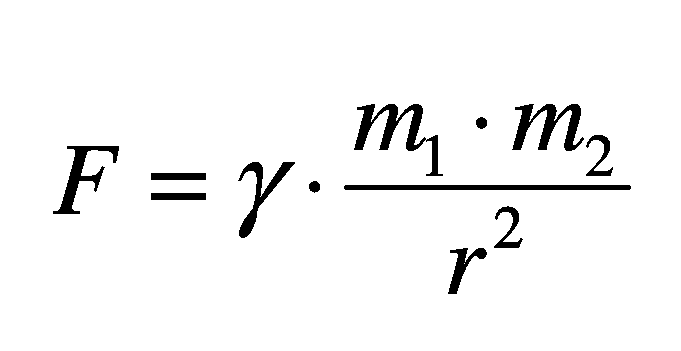Поимите маса и тежина на некое тело вообичаено се поистоветуваат во секојдневниот живот, меѓутоа физички гледано, тоа е неисправно, бидејќи тие се два наполно различни физички поими, и како такви се изразуваат со различни основни мерни единици! Па, да ја објасниме разликата меѓу нив!
Масата “m" е скаларна големина. Всушност таа е својство на сите тела да ја задржат нивната состојба во којашто моментално се наоѓаат, т.е. ако мируваат да останат во мирување, а ако се движат, да останат во рамномерно праволиниско движење. Според тоа, масата е мерка на тромоста (инерцијата) на телата, а основна мерна единица за маса е kg.
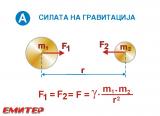
Сега следува најбитното: помеѓу две блиски тела (маси) владее заемно привлечна сила, т.н. гравитација (види приказ А на сликите во прилог), па тие маси се стремат меѓусебно да се приближуваат. Нивната заемно привлечна сила F е дефинирана со Њутновиот закон за гравитација:
каде што: γ – гравитациска константа
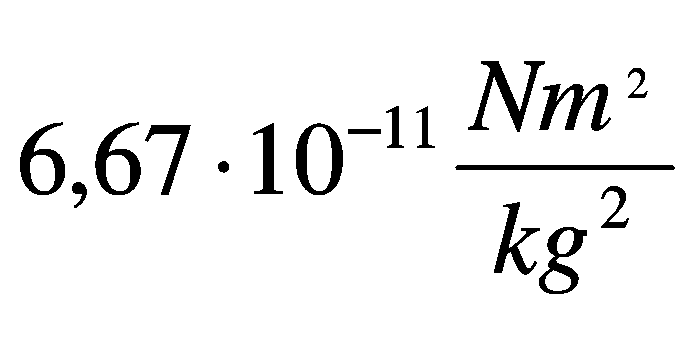 ;
;
m1 и m2– маси на телата;
r – растојание помеѓу центрите на масите.
Секоја сила, при дејството на некое тело, креира забрзување во движењето на тоа тело, а односот меѓу силата и забрзувањето е позната како II Њутнов закон. Во неговата општа форма, тој закон гласи:
F = m · a
каде F – сила, m – маса, a – забрзување.
Сега, да претпоставиме дека едно од двете наведени тела е нашата Земја. Нејзината огромна маса има огромна тромост, па таа нема да се поместува кон второто тело со мала маса, туку телото со мала маса ќе се поместува кон Земјата. Тоа поместување, со други зборови, ние го нарекуваме “слободно паѓање” кон Земјата, всушност, рамномерно забрзано движење под дејство на гравитацијата. Во склад со тоа, наведената равенка од II Њутнов закон се изразува во облик:
G = m ·g
каде што G – гравитациска сила,
g – гравитациско забрзување (на Земјината површина g = 9,81m/s2).
Кога телото ќе падне на тлото на Земјата, гравитациската сила G ќе продолжи да дејствува помеѓу телото и тлото на Земјата, а токму тоа ние го нарекуваме “тежина” на телото.
Значи тежината на телото е сила, па според тоа, таа е векторска големина. Имено, освен големина, таа има и насока на дејствување. Основна мерна единица за секоја сила, па и за тежината е Њутн (Newton) и се означува со N.
За крај, ќе ја пресметаме тежината на едно тело (на пример, човечко тело) со маса m=75 kg во три различни космички средини!
1) Ако тоа тело лежи (стои) на површината на Земјата (g = 9,81m/s2), неговата тежина според формулата G = m ·g изнесува G = 75 · 9,81 = 735,75 N. Вагите со коишто се мери телесната тежина, всушност, мерат тежина, а не маса, но нивната скала (бројчаник) е калибрирана да ја покажува еквивалентната маса – во овој случај 75 kg.
2) Ако истото тоа тело се наоѓа на површината на Месечината (g = 1,635m/s2), неговата тежина би изнесувала G = 75 · 1,635 = 122,63 N, односно 6 пати помалку отколку на Земјата! Вагата (со пружина) во овој случај би покажала само 12,4 kg кога астронаутот би застанал на неа!
3) Истото тоа тело во далечен слободен космички простор каде што речиси нема гравитациско забрзување (g = 0), би имало тежина G = 75 · 0 = 0 N, значи тоа би било во безтежинска состоjба!
Ете ја разликата меѓу масата и тежината; за една иста маса добивме 3 различни износи за тежина, во 3 различни космички средини! (види го приказот Б на сликите во прилог).